-- Main.estate - 13 Nov 2012
Consider a point process 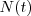 , which counts in time the number of failures up to time
, which counts in time the number of failures up to time 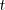 . At each failure the item is instantly repaired and as a result, its current failure rate becomes
. At each failure the item is instantly repaired and as a result, its current failure rate becomes  times smaller. How does this process evolve in time? -- at one hand, the ``baseline" failure rate
times smaller. How does this process evolve in time? -- at one hand, the ``baseline" failure rate  will typically increase in time, but on the other hand, multiplication by
will typically increase in time, but on the other hand, multiplication by  each time will pull it down. So, what will be the result?
In other words, if
each time will pull it down. So, what will be the result?
In other words, if 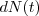 is the ``small" increment forward, or the number of failures in
is the ``small" increment forward, or the number of failures in ![$[t, t+dt]$](/foswiki/pub/Users/Estate/FailureWithRepairs/latex6a92e142bd44882df3ea39e7a63d161c.png) for small
for small 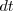 , and if
, and if  is some ``baseline" failure rate, then this
is some ``baseline" failure rate, then this 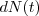 is a Poisson random variable with parameter
is a Poisson random variable with parameter 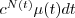 , that is, essentially, the probability of a failure occurring in this interval is
, that is, essentially, the probability of a failure occurring in this interval is 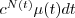 , and the process with increment
, and the process with increment
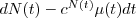 is a martingale.
The model can be very naturally generalized to make
is a martingale.
The model can be very naturally generalized to make  random and/or make it changing in time.
It seems that the applications of this model will be numerous, and its mathematical analysis not too simple.
random and/or make it changing in time.
It seems that the applications of this model will be numerous, and its mathematical analysis not too simple.
 Users/Estate
Users/Estate