Research

Menu:

I seem to fill my time without too much effort. I'm largely interested in geometry, analysis, and their applications, but I've been getting more and more involved in conservation research over the past few years, particularly bioacoustics.
More information can generally be found in my publications, but some general headings are:

AviaNZ: Bioacoustics

I'm a bird nerd, and have managed to combine my research and hobby by working on population estimation by unobtrusive monitoring. This is primarily based on passive acoustic monitoring, mathematical analysis of sound, and behavioural ecology. I'm also an accredited kiwi practitioner, science advisor for the South Island Kākako Trust, volunteer at Zealandia ecosanctuary, and have worked with the Kākāpō Recovery Group. I'm a 2021 National Geographic Explorer. Our open-source software, and much more information, is available on our wepage.

Euler Equations on Diffeo Groups

I have a long-standing interest in the geometric and analytic aspects of generalised Euler equations on diffeomorphism groups. The focus is a better understanding of the equations and their behaviour. This is part of the field of shape analysis, which was motivated by the work of D'Arcy Wentworth Thompson in `On Growth and Form'. (Picture is my brain, sometimes it's nice to know you have one!)

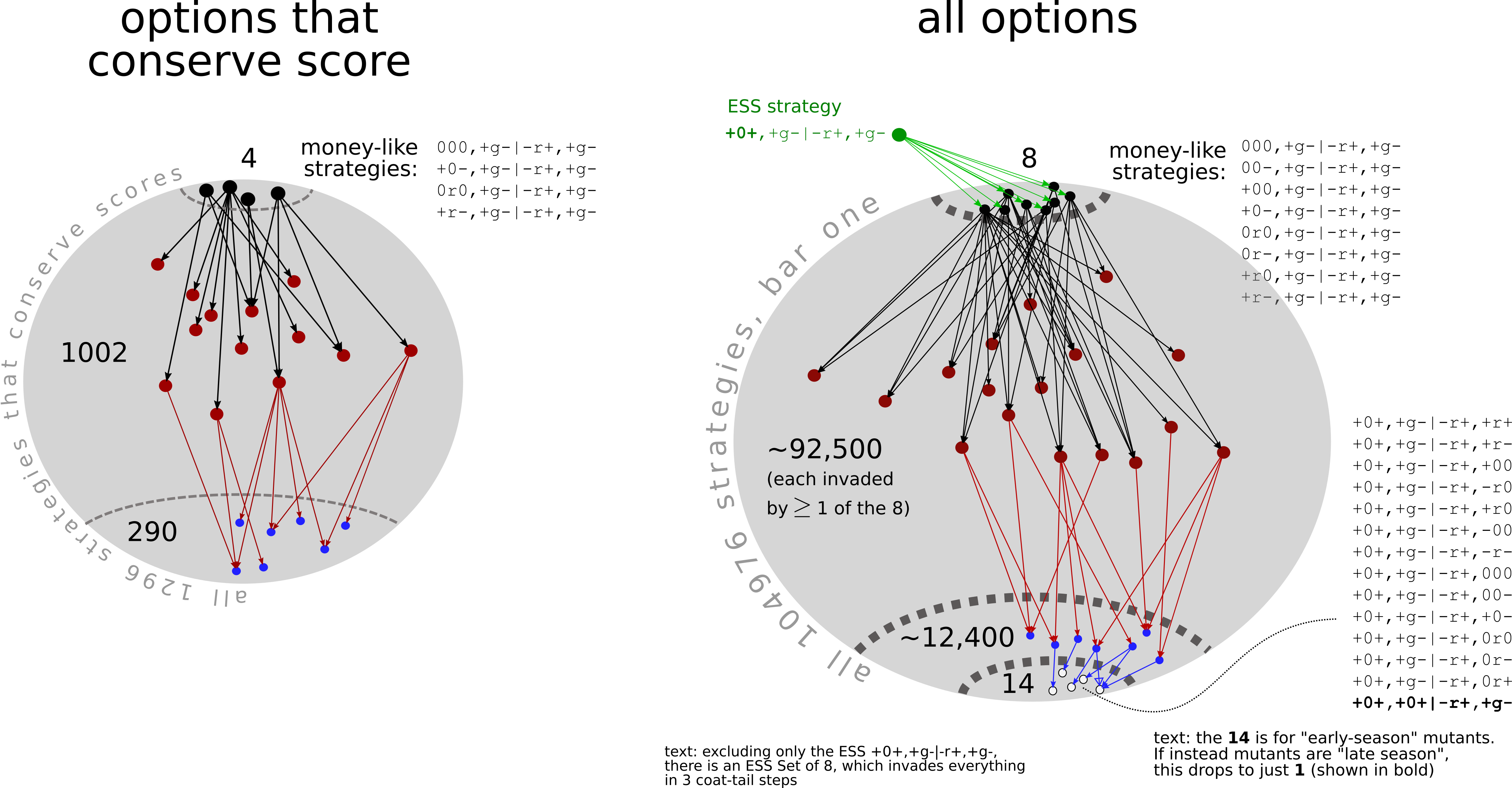
Stochastic Game Theory

Together with Marcus Frean I'm interested in evolutionary game theory, particularly why things arise -- small things like money and sexual reproduction. (Picture from our paper about score-mediated indirect reciprocity.)

Information Geometry and Machine Learning

Understanding why machine learning algorithms work is very interesting. One approach is to consider either the manifolds on which data live, or the manifolds where the parameteric distributions underlying them live, and to write down mathematical formulations of the algorithms. I'm also interesting in using the algorithms in conservation technology. (Picture from http://www.nada.kth.se/~asa/Game/BigIdeas/ai.html)