Welcome to Yi Mei's homepage
For what will it profit a man if he gains the whole world and forfeits his soul?-- Matthew 16:26
Large Scale Optimization with Interdependent Modules
It is an era of Big Data. A huge number of data can be collected through social network, transaction record, mobile sensor, etc. However, it is still an open question how to make the best use of the big data, that is, recognize the useful patterns that can lead to more efficient strategic decisions (e.g., personalized recommendation and promotion, real-time adaptive decision making such as re-routing and re-scheduling) in the future. This problem can be essentially seen as large scale optimization (e.g., maximizing the accuracy or minimzing the error of the model).
When dealing with a huge amount of data, traditional optimization techniques are no longer available, as they might take forever to obtain a solution. In this scenario, a commonly used strategy is divide-and-conquer, which identifies smaller modules from the whole problem, and then tackles them individually or coordinately. This way, one can dramatically reduce the search space and thus the computational effort without losing much the solution quality.
If the modules are independent and small enough, then Bingo! However, this is usually not the case in reality. In fact, a complex system normally consists of interdependent modules. For example, in supply chain, the material delivery and product manufacturing modules interact with each other. Therefore, when dealing with this type of problems, the following two open questions are to be answered:
- How to decompose the problem into modules with minimal inter-dependence?
- How to design efficient coordinate optimization algorithms rather than optimizing the modules individually?
Examples
Supply Chain

There are a number of sub-problems in supply chain management, such as product manufacturing, storing and distribution. Each sub-problem is complex by itself, and they interact with each other. If the sub-problems are solved separately, one cannot expect a promising outcome since the interactions between them are ignored. On the other hand, it is hardly possible to solve all the sub-problems as a whole due to the high complexity. A more effective solution should be in between, i.e., decomposing the entire problem into smaller sub-problems and coordinating the optimization of the sub-problems by taking the interactions into account.
To facilitate the investigation of the interactions between sub-problems, a benchmark problem called the Travelling Thief Problem is proposed. It is a combination of the well-known Travelling Salesman Problem (TSP) and Knapsack Problem (KP). The objective function is specifically designed to create a complex interaction between the TSP and KP sub-problems. Details of this interesting problem can be found here.
We have conducted several studies on this problem and developed intelligent decomposition and optimization algorithms for solving it. A recent work has won the 2nd Prize of the CEC Competition at IEEE WCCI 2014: Optimisation of Problems with Multiple Interdependent Components, 2014. An improved work can be found here.
Rosenbrock Function
Rosenbrock function is an interesting benchmark function for those who like pure theoretical investigation. Its formula is given as follows:
 .
.
For the 2-dimensional case, the fitness landscape is
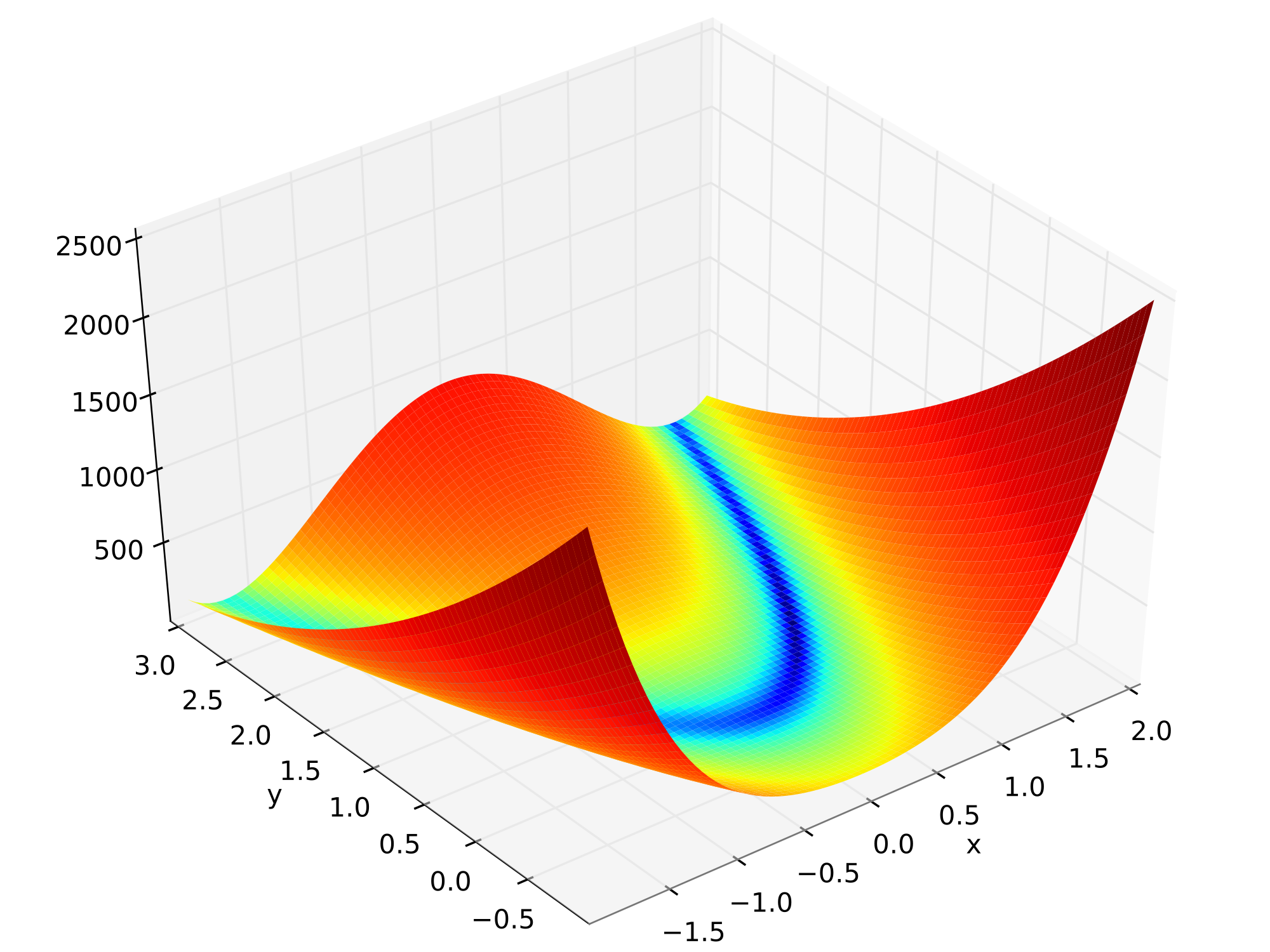
Rosenbrock function has an interesting chain-like interaction between variables. That is, xi only interacts with xi-1 and xi+1, but is independent of all the other variables. Such property makes Rosenbrock function a fully non-separable function, whose interaction matrix is quite sparse. The existing studies have shown that optimizing Rosenbrock function as a whole cannot lead to an appealing performance. Then, it would be desirable to find a proper decomposition of the function along with a strategy to handle the weak interaction between the resultant sub-problems.
We proposed a Differential Grouping decomposition strategy lately, which performed perfectly in identifying independent sub-problems. Combining with CMA-ES, which is the state-of-the-art optimization algorithm for small to medium sized problems, we achieved much better results on the IEEE Large Scale Global Optimization benchmark functions, as shown in this paper. We are trying to extend it to interacting sub-problems.
Publications
Below are my publications relevant to large scale global optimization.
Note:
- Publications listed below are made on-line available for faster dissemination. The copyright of the papers is owned by their publisher.
- All the codes are provided to help empirical comparison and understand the idea of the work. We guarantee them to be the original code from which the results in the papers were obtained (there is no trick). Please do NOT misuse them. We'd appreciate it if you cite the relevant paper when using the codes.
Journals
Yi Mei, Mohammad Nabi Omidvar, Xiaodong Li, and Xin Yao, "Competitive Divide-and-Conquer Algorithm for Unconstrained Large Scale Black-Box Optimization," ACM Transactions on Mathematical Software, Accepted, June, 2015.
The MATLAB code of the proposed DG-CMA-ES algorithm can be downloaded here.Yi Mei, Xiaodong Li, and Xin Yao, "On Investigation of Interdependence Between Sub-problems of the Travelling Thief Problem," Soft Computing, DOI: 10.1007/s00500-014-1487-2, October, 2014.
Mohammad Nabi Omidvar, Xiaodong Li, Yi Mei, and Xin Yao, "Cooperative Co-evolution with Differential Grouping for Large Scale Optimization," IEEE Transactions on Evolutionary Computation, vol. 18, no. 3, pp. 378-393, 2014.
The MATLAB code of the differential grouping algorithm can be downloaded here.
Conference Proceedings
Yi Mei, Xiaodong Li, Flora Salim and Xin Yao, "Heuristic Evolution with Genetic Programming for Traveling Thief Problem," Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC2015), Sendai, Japan, 25-28 May, 2015.
Yi Mei, Xiaodong Li and Xin Yao, "Improving Efficiency of Heuristics for the Large Scale Traveling Thief Problem," Lecture Notes in Computer Science (SEAL2014), vol. 8886, pp. 631-643, 2014.
The source code (Shell script plus C++) can be downloaded here.Mohammad Nabi Omidvar, Yi Mei and Xiaodong Li, "Effective Decomposition of Large-Scale Separable Continuous Functions for Cooperative Co-evolutionary Algorithms," Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC2014), pp. 1305-1312, Beijing, China, 6-11 July 2014.