Main Page | Alex's SSI references | Forum
I should point out that the opinions expressed here are my own and that I accept no liability for mistakes and/or omissions: caveat lector. A Standard disclaimer applies.
Back

Honours | Calendar | References (Normal) (Formal) (Quick) (Links only) (BibTeX) (Light Toggle)

Total of 42 records found.
Current page is: file:///C:/My Documents/Education/University/public_html/comp432.html?HTML=true&
File is: comp432_lite.html

Sort by Category, type, title, short_title, author, pub_date, read_date, rank. View rank.

[LN] Title: COMP 432: Functional Programming - Lecture Notes
Author(s): Neil Leslie
Publication Date: (2002) - Publisher: Centre for Logic, Language and Computation, MCS, VUW.
Remote: http://www.mcs.vuw.ac.nz
Comments: Lecture notes.

[FPM] Title: Why Functional Proramming Matters
Author(s): John Hughes
Publication Date: (1984) - Publisher: Institution för Datavetenskap.
Found/Read: 2002/02/26
Comments: Functional programming has good glue. A Paper on how Functional Programming has strong support for Modularity [comp462 MOD] via higher-order functions [HOF] and lazy evaluation [LE]. The Newton-Rapson algorithm for computing approximations to the square root of a number N, Numericial differention and integration, and α-β pruning are given as examples.
"Modular design brings with it great productivity improvements. First of all, small modules can be coded quickly and easily. Secondly, general modules can be re-used, leading to faster development of subsequent programs. Thirdly, the modules of a program can be tested independently, helping to reduce the time spent debugging."
"Our ability to decompose a problem into parts depends on our abilty to glue solutions together."
"Smaller and more general modules can be reused more widely, easing subsequent programming."

[HOF] Title: Higher-order function
Comments: A function that takes function-valued arguments or which returns a function as a result.
We can lift out common functionality (patterns) of a group of functions and generalise them using one higher order function [POLY]. Hence increasing the modularity, making reuse easier.
They make it easier to quickly define new functions for datatypes.
Examples of uses include function composition and the map function.
Function composition allows other functions to be joined together to make larger (more powerful) functions. - Less programming required due to greater modularity.

See also [FPM]

[LE] Title: Lazy Evaluation
Comments: Lazy evaluation only does as much computation as is really needed. Laziness allows us to generate the input only as needed, and to reclaim storage as it becomes free, thus giving a useful optimisation - [LN]. Helps support Modularity. Allows functions to work with large (potentially/actually infinte) data structures. Generate/calculate only as much is needed to evaluate expression.
Remarkable property: if any evaluation strategy finds a value of an expression then leftmost, outermost will.
From [LN] - When we use lazy evaluation:

1. we only evaluate as expression if we have to; - handled by normal order evaluation [RS].
2. we only evaluate an expressing as far as we have to; - handled by evaluating to [WHNF].
3. we only evaluate an expression once. - handled by representing λ-terms as graphs, rather than trees.

• don't go there if you don't have to.
• don't go to far (Weak Head Normal Form)
• don't go there twice ( f(27) + f (27) )

Examples of the usefulness of lazy evaluation include Newton-Raphson algorithm for computing approximations to the square root of a number N, α-β pruning...

See also [FPM]

[DFVSI] Title: Debate: Functional vs Imperative
Remote: http://www.cs.nott.ac.uk/~pni/FP/fp-sections.html
Comments:

"Programmers practiced in imperative languages are used to a certain style of programming. For a given task, the imperative solution may leap immediately to mind or be found in a handy textbook, while a comparable functional solution may require considerable effort to find (even if once found it is more elegant). And though there are a large range of problems that possess efficient solutions in a functional language, there remain some tough nuts for which the best known solutions are imperative in style. (For these reasons, many functional languages provide an escape to the imperative style, for instance Standard ML includes updatable references as a basic data type, and Haskell provides them via monads.)"

Philip Wadler. Functional Programming: Why no one uses functional languages.
SIGPLAN Notices 33(8):23-27, August 1998.

[REDEX] Title: REDEX - reducable expression
Comments: From Lecture notes [LN] - "A redex is a reducible expression, that is, an occurrence of an application on an abstraction ( (λx.M)N )."
It is a site where a β-reduction [BR] can be performed. (λx.M)N

See also [ULC]

[EO] Title: Evaluation Order
Remote: http://foldoc.doc.ic.ac.uk/foldoc/foldoc.cgi?lazy+evaluation
Comments: Haskell uses leftmost, outermost in performing Lazy Evaluation [LE]. Leftmost, outermost (a.k.a. normal order evaluation - call-by-value) has that property that: "is any evaluation strategy finds a value of an expression then leftmost, outermost will." - [LN]. In contrast to normal order evaluation, and used by most imperative languages, is applicative order evaluation (call-by-value)- evaluate the arguments to a function before evaluating the function.
See Also [REDEX]

[ZIPN] Title: Heterogeneous container types. ZipN problem.
Comments: Zip :: n -> Tuple(n) -> [Tuple(n)]
Type declarations like this make it difficult (if not impossible) to do type inferance.
"The number of times a constructor is applied must be known at compile time and, hence, be fixed in the program text. Tuples are a conspicuous example. The tuple (a,b) does not have the same type as the tuple (a,b,c). There is no way to write a function entuple n a that builds a tuple (a,…,a) of length n. Another example is the zip problem: we have zip2, zip3, but there is no generic zipN in the current type systems implemented in functional languages." - [DFVSI]

Haskell's type system is just not expressive enough to allow us to express structural recursion for any inductively defined type.
Functions can't take types as arguments, nor (apart from the use of type classes) have types which depend on values supplied to the function. - [LN] (2001)

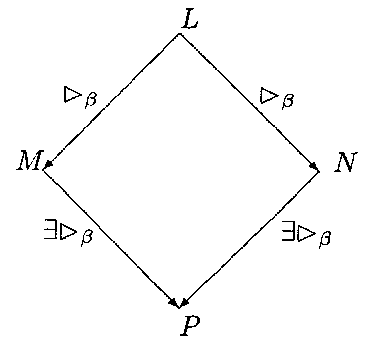
[CR] Title: Church-Rosser property/Theorem
Comments: a.k.a The diamond property, confluence.
"if two evaluation strategies reduce a λ-term to a normal form, then these normal forms are the same." - [LN] (Normal forms are unique).
Theorem 1 If L >_β M and L >_β N then there is some P such that M >_β P and N >_β P.

Proof in lecture notes [LN] p.g. 100:
Lemma: If a relation has the diamond property then so does its transitive closure.
Define a reduction relation —» on λ-terms such that:

• —» is confluent (has the diamond property);
• the transitive closure of —» is >_β.

Corollary 1.1 If M =_β N then there is some P such that M >_β P and N >_β P.
Corollary 1.2 Normal forms are unique: any term which can be reduced to normal form can only be reduced to one normal form. The normal form of a term is also the value of the term.
Collary 1.3 The λ-calculus is consistent. Cannot show P =_β Q, for all P, Q.

See also [BR]

[SA] Title: Strictness analysis - Questions Chapter 4
Author(s): Philip Wadler
Remote: http://www.research.avayalabs.com/user/wadler/topics/strictness-analysis.html
Comments: "Analysing time complexity of functional programs in a lazy language is problematic, because the time required to evaluate a function depends on how much of the result is "needed" in the computation. Recent results in strictness analysis provide a formalisation of this notion of "need", and thus can be adapted to analyse time complexity."

[LC] Title: list comprehension
Remote: http://haskell.cs.yale.edu/haskell-report/tutorial.html
Comments: A powerful and succinct way to describes lists that uses a generate-and-test mechanism.
list comprehension <= [ expression | generator [, generator]* [, test]*]
generator <= pattern <- list
test <= Bool

Quicksort example from lecture notes [LN]
quick :: Ord a => [a] -> [a]
quick [] = []
quick (h:t) = quick [x | x <- t, x < h] ++
        h :
        quick [x | x <- t, x >= h]

[MLWP] Title: ML for the Working Programmer
Author(s): Paulson, L. C.
Publication Date: (1991) - Publisher: Cambridge Universty Press, Cambridge, England..
Comments: On comparing functions - "Correctness must come first. Clarity must usually come second and efficency third. Whenever you sacrifice clarity for efficiency, by sure to measure the improvement in performance and decide whether the sacrifice is worth it. A judicious mixture or realism and principle, with plenty of patience, makes for efficent programs."
Efficency is mainly a problem for the compiler.

[HM] Title: Hindley-Milner system for Type variables
Comments: From [LN] - In the Hindley-Milner system:

1. every typable term has a principle type [PT];
2. principal types, being principle, are unique.

Furthermore, given any term:

1. it is possible to say whether it is typable;
2. if the term is typable, it is possible to give the principal type.

Thus allowing for type inference or a principal type algorithm.
From the programmers perspective, type inference with polymorphic typing gives the security of a type system with much of the flexibility of an un-typed language.

[PT] Title: Principal Type
Found/Read: 2002/05/23
Comments: Type inference - "Every typable term has a principle type. The principal type is the most general type that a term can have, in the sense that every type which a term can have is an instance of the principle type."
A principal type algorithm takes a λ-calculus term and returns either:
The principal type of the term; or
The information that the term has no type.

In the λ-calculus, any typable term has a normal form. Hence, typing implies termination. A program could be checked for termination properties by the compiler at compile time.

See also [TLC] [HM]

[TYPE] Title: Types and Typing
Comments: Types provide information to the programmer and compiler (writer):

1. Typing reduces errors
2. Errors are picked up at compile time
3. Bridge between syntax and semantics

∀α.α → α - α is a.k.a a type variable, which is used to signify that the property is valid for any instance of the variable.
"Haskell has a higher-order [HOF], polymorphic [POLY] type system, …" - [LN]
"A type like a -> a is implicitly universally quantified over types." - [NC]. Here a is a variable that ranges over types.
Type inference [HM] with polymorphic typoing gives the programmer the security of a type system with much of the flexibilty of an un-typed language.
Type classes "let us make ad hoc polymorphism less ad hoc" - [LN]. The use of type classes lets us express the similarites, while hiding the details of the differences.

See also [SYNO] [DATA] [TLC]

[SYNO] Title: Type Synonyms
Comments: type String = [Char] - a new name for an existing type.

[TC] Title: Type class
Comments: From [LN]:
"A class is a collection of types. A type which is in a class is called an instance of that class. Classes can be derived from other classes. The derived class inherits operations."
Ever class has a signature which comes from the functions it can perform.
Type classes and type variables [TYPE] both contribute towards parametric polymorhism [POLY].

[DATA] Title: Data Type
Comments: data Fruit = Kiwi | Apple | Banana | Pear - a new type.

[AT] Title: Algebraic Types
Comments: Pg. 41 in [LN]. Types that are defined in terms of their constructors.
Algebraic Meaning: [www.dictionary.com]

1. Of, relating to, or designating algebra.
2. Designating an expression, equation, or function in which only numbers, letters, and arithmetic operations are contained or used.

Tagged Unions: data Either a b = Taga a | Tagb b

[CLASS] Title: Class
Comments: From [LN] pg 38 - A class is a collection ot types [TYPES]. A type which is in a class is called an instance of that class. Classes can be derived from other classes. The derived class inherits operations. Eg. Eq, Ord, Enum, Bounded
Classes are declared with a type signature

[POLY] Title: Polymorphism
Remote: http://foldoc.doc.ic.ac.uk/foldoc/foldoc.cgi?query=polymorphism
Comments: Parametric Polymorphism - Using the same algorithm for different types - is based on universal quantification at the level of types.
Ad Hoc Polymorphism (overloading - existential quantification over types) - same name for different functions depending on the type - uses type classes to express the similarities between properties of functions, while hiding the details of the differences - [LN].
See Also [comp462 POLY]

[ADT] Title: Abstract Data Types
Found/Read: 2002/04/16
Comments: From [LN] pg. 51.
There are various more-or-less equivalent definitions of ADT's in the literature:

• An ADT is 'a type, and a collection of functions on that type' (Okasaki, 1998);
• 'An abstract type consists of the type name, the signature of the type, and the implementation equations for the names in the signature' (Thompson, 1999);
• 'An abstract data type consists of a type together with a explicit set of operations, which are the only means by which to compute with values of that type [comp462 ENCAP].' (Paulson, 1991).

In Haskell information hiding is achieved by using modules [MOD].

[MOD] Title: Module
Found/Read: 2002/04/16
Comments: A tool to impose scope and hide information - keep local information local, and export an interface.
module Name
( export function list (without types)
.
.
) where
implementation - functions/equations

[PAT] Title: Patterns
Remote: http://www.haskell.org/tutorial/patterns.html
Found/Read: 2002/04/16
Comments: as-pattern
f s@(x:xs) = x:s
rather than:
f (x:xs) = x:x:xs

[ULC] Title: The untyped λ-calculus
Author(s): Alonzo Church
Found/Read: 2002/05/09
Comments: One of the first formal models of computation.
Lecture notes [LN] pg 91:
Term → (Var) - a variable - also called atomic.
| (λVar.Term) - an abstraction of a variable over some term - a.k.a. compound terms
| (Term)(Term) - the application of a term to a term - a.k.a. compound terms

Var → x,y,z,… - a.k.a. atomic
Conventions ([LN] pg.91):

• we omit the outer brackets
• application associates to the left, so we can write L M N rather than (L M) N
• abstraction associates to the right, so we can write λx.λy.λz.M rather than λx.(λy.(λz.M))
• we allow one λ to stand for many, and write λxyz.M rather than λx.λy.λz.M
• application binds tighter that abstraction, so we write λx.M N rather than λx.(M N)

(Lecture Notes [LN] pg 92):
Rules for equality: Reflexivity, Symmetry, Transitivity, Application of the same term to the left or right, and Abstraction by the same variable.
Length of term = Number of occurences of variables in the term (inductive).
Subterms = the term itself ∪ the subterms of the components of the term.
Occurrence "A term N occurs in a term M at a location …" defined by a "… path through the λ-term (considered as a tree) required to get there." λx - an abstractor, with the occurrence of x in an abstractor called a binding occurrence. Varialbes in terms that aren't binding occurrences are called non-binding occurrences.
Components - all occurrences of terms in M that are not binding occurrences of variables.
Scope - P is the body of λx.P and the scope of abstractor λx.
Every occurrence of a varible in a term is one of:

• a binding occurrence - λx
• a bound occurrence - λx(… x …)
• a free occurrence - λx…λy(…z…)

x(λx.x) ≡ x(λy.y) - a varialbe may be both free and bound in a term (depends on occurrence)

[COMB] Title: Combinator
Comments: From Lecture Notes [LN] - "A term in which no variable occurs free is called (a) closed term or a combinator."

[AC] Title: α convertibility
Comments: From Lecture Notes [LN] - "Two terms which differ only in the names of their bound variables are said to be α-convertible."
Two α-convertible terms are considered to be the same term and hence syntactically identical. I.e. λx.x ≡ λy.y

[BVC] Title: Bound Variable Clashes
Comments: From Lecture Notes [LN] - "A term M in which an abstractor λx occurs, and in which a varible x occurs outside the scope of the abstractor…"
λx.λx.x ≡ λy.λx.y or
λx.λx.x ≡ λx.λy.y
Scope with holes - variables are bound by cloest abstractor, making the second interertation correct.

[DBT] Title: De Bruijn terms
Found/Read: 2002/05/14
Comments: Lecture Notes [LN] p.g. 95 - a notation where bound variables are not named.
λx.λy.x(λz.y z w) becomes λλ1(λ234)
λx.(λy.y x)(λz.z x) becomes λ(λ2 1)(λ2 1)

[SUB] Title: Substitution
Found/Read: 2002/05/14
Comments: Lecture Notes [LN] p.g. 96
[N/x]M means 'substitute N for x in M' or 'replace x with N in M'.
"When we substitute a term N into an abstraction we must take care that no free variable in N comes into scope of the abstractor." So [x/y]λx.x y ≡ λv.v x; rather than λx.x x which is different.

[CONV] Title: Conversions
Comments: Lecture Notes [LN] p.g. 97

See also [BR] [REDEX]

[BR] Title: β reduction
Comments: From Lecture Notes [LN] p.g. 98 - (λx.M)N >_1β [N/x]M - a single step of β reduction. [SUB]
>_β "denotes a sequence of (possibly empty) β-reductions." - (> should really be a triangle - ▹).
β-reduction is reversed by β-expanssion.
L =_β M if L can be converted to M using a sequence of β reductions and/or expansions.

See also [CR]

[ER] Title: η reduction
Comments: From Lecture Notes [LN] p.g. 105 - λx.(Mx) >_1η M x ¬εFV(M)

[RS] Title: Reduction Strategies - Leftmost, Outermost
Found/Read: 2002/05/21
Comments: From lecture notes [LN] p.g. 100.
"The leftmost redex [REDEX] of a term P is the redex whose parenthesis is to the left of all other parentheses of redexes in P. The leftmost reduction of a term P is the sequence of terms generated from P by reducing the leftmost redex of each term generated."
Theorem 2 A term has a normal form if and only if its leftmost reduction is finite. The last term in the reduction is the normal form.
If any evaluation strategy finds a value on an expression then leftmost, outermost (a.k.a normal order evaluation) will.

See also [LE]

[NF] Title: Normal Form
Comments: From lecture notes [LN] p.g. 100.
"A term is in normal form (NF) if it contains no redexes [REDEX]."
Hence >_β [BR] will not affect a term in normal form - leading to corollary 1.2 in [CR].
NF => [HNF] => [WHNF] (but not necessarily vice versa).

[HNF] Title: Head Normal Form
Comments: A term is in head normal form (HNF) if it is of the form λx₁…x_n.xM₁…M_m where n, m ≥ 0.

See also [NF] [WHNF]

[WHNF] Title: Weak Head Normal Form
Comments: A term is in weak head normal form (WHNF) if it is of the form λx₁…x_n.xM₁…M_m where n, m ≥ 0, m > n.
Put another way, an expression in WHNF has no top-level redex [REDEX]. Left-most outermost reduction [RS] will reduce an expression to WHNF before it reduces it to NF. Stopping reduction when we reach WHNF allows us to start producing output before the evaluation of a program is finished - [LN] (2001).
Examples from Haskell in WHNF:
4
(3 + 4) : [1..]
(3 +)
hd

See also [NF] [HNF]

[HASK] Title: Haskell
Remote: http://www.haskell.org
Comments: Our favourite functional programming language.
The λ-calculus provides us with a model for Haskell.

See also [ULC]

[LD] Title: λ-definabilty
Comments: Lecture Notes [LN] p.g. 103 - The outline of a proof that recursively definable functions are λdefinable.
A recursive function:
Includes the initial functions:

• zero Z(n) = 0
• successor Succ(n) = n + 1
• projections P_iⁿ (x₁,...,x_n) = x_i

Is closed under:

• composition
• primative recursion
• minimisation

Fix-point finders, Theorem 3 (∀F) (∃X) (X >_β FX)

[RFPF] Title: Recursion via fix-point finders
Comments: [LN] pg 103] A fixpoint is a value such that the function applied to that value gives back the value.
The Y combinator [COMB] is used in Theorem 3 of [LD]

[TLC] Title: Typed λ-calculus
Comments: Any typable term has a normal form and hence typing implies termination. This allows termination properties to be cheecked at compile time.
Fix-point finders can't be typed.
Types for λ-terms:Type → (Type → Type)
| TyVar
TyVar → a,b,c,... - endless stock of variables
Associates to the right - α → β → γ instead of α → (β → γ)
Type assignment M : τ - M has type x (often within a context.)
Type context or environment is a set of type assignments denoted by upper-case Greek letters Γ, Δ ...

[MONAD] Title: Monad
Found/Read: 2002/05/28
Comments: Ideally, an expression will only have one unique value (x -> x == x)(Referential transparency)
Type () only has the value (). IO () only returns () as its value.
getLine :: IO String
getChar :: IO Char
putStr :: String -> IO ()
return :: a -> IO a
do notation - allows for the composition of I/O actions. In construction with a if-then-else statement
<- (single assignment) allows for the naming of the result of a IO action.
>>= :: IO a -> (a -> IO b) -> IO b.(bind) passes teh result of the first IO operation to the second.
>> :: IO a -> IO b -> b (forgetful bind) throws away value of first operand.

^Top^

Honours | Calendar | References (Normal) (Formal) (Quick) (Links only) (BibTeX) (Light Toggle)