Suppose a positive random variable 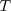 with an absolutely continouse distribution
with an absolutely continouse distribution 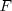 is our model for duration of life of an individual; consider the so called "excess life distribution"
is our model for duration of life of an individual; consider the so called "excess life distribution"
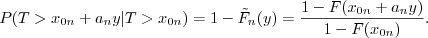 This is a very interesting object to study when we speak abut longevity: what is the probability that the individual will live longer than
This is a very interesting object to study when we speak abut longevity: what is the probability that the individual will live longer than 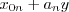 , given that
this individual already lived for longer than
, given that
this individual already lived for longer than 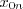 . It is especially interesting to study when
. It is especially interesting to study when 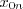 is large.
According to the so-called Balkemaa-de Haan-Pickands theorem, if there is a sequence of constants
is large.
According to the so-called Balkemaa-de Haan-Pickands theorem, if there is a sequence of constants 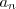 such that for
such that for  there is a limit,
there is a limit,
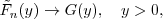 then this
then this 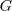 can only be of the following form:
can only be of the following form:
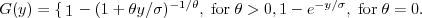 Now we follow what is said in the book DemgraphyBook, Lecture 15.1*:
Denote
Now we follow what is said in the book DemgraphyBook, Lecture 15.1*:
Denote ![$\mu(z) = f(z)/[1-F(z)]$](/foswiki/pub/Users/Estate/TailsDemography/latex9349c9c411326fcd87542fd9b0330549.png) is the force of mortality, corresponding to the distribution
is the force of mortality, corresponding to the distribution 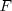 . If the asymptotic relation
. If the asymptotic relation
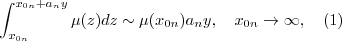 holds, the only choice for
holds, the only choice for 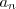 is
is 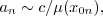 with
with  a generic notation for constant, and the only possible limit for
a generic notation for constant, and the only possible limit for  is the exponential distribution:
is the exponential distribution:
![$$ 1- \tilde F_n (y) \to \exp [- c y] . $$](/foswiki/pub/Users/Estate/TailsDemography/latex21236d34f4b7ec66b08910d40a97921a.png) What is unusual and needs investigation is this: the (1) is true for all distributions we discussed in the book, and yet the longevity data (for those over 90) for New Zealand population, does not quite agree with the exponential distribution it has to follow. Moreover, serious researchers studied similar data on longevity in other countries and also suggested long tail distribution above. But ... (1) is true and the limit must be exponential :-). Of course, one should understand what is happening.
What is unusual and needs investigation is this: the (1) is true for all distributions we discussed in the book, and yet the longevity data (for those over 90) for New Zealand population, does not quite agree with the exponential distribution it has to follow. Moreover, serious researchers studied similar data on longevity in other countries and also suggested long tail distribution above. But ... (1) is true and the limit must be exponential :-). Of course, one should understand what is happening.