Imagine particles running on the screen, changing color as they get "older", appearing, disappearing. In a word - imagine a toy model for a population. It will be not only fascinating to watch, it will be useful in many ways: in analysis of the age structure, in tracing how a change in social habits will influence the population, in population forecasting, etc.
However, if you start with a simple model for marked point process 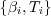 , where
, where 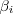 is the birth moment of the i -th born individual and
is the birth moment of the i -th born individual and 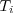 is duration of the individual's life, then not only theory becomes transparent but also its computer implementation becomes easy.
The project can go very long way and can incorporate the models for mixtures of distributions and migrations. The computer models like this, based on good mathematics, will be useful not only for human populations, but for many other biological populations. Population of bank accounts - another interesting popualtion.
is duration of the individual's life, then not only theory becomes transparent but also its computer implementation becomes easy.
The project can go very long way and can incorporate the models for mixtures of distributions and migrations. The computer models like this, based on good mathematics, will be useful not only for human populations, but for many other biological populations. Population of bank accounts - another interesting popualtion.